[10000ダウンロード済み√] ���の半径の求め方 高校 公�� 343353-円の半径の求め方 ��校 公式

 「円周の長さ = 直径 × 円周率」 っていう計算式が公式としてのっているね。 たとえば、直径3cmの円があったとすると、円周の長さは、 3 × 314 = 942 cm になる。 つまり、この 円の面積の求め方 円の面積を求めるときは 円の面積 = 半径 × 半径 × 円周率 という公式を使います。 たとえば、半径が 3 c m の円の面積は 半径 半径 円周率 半 径 × 半 径 × 円 周 率 = 円の面積と円周の求め方（公式） 続いて、円の面積と円周の長さを求める公式をご紹介します。 円の面積と半径 円の面積 (S) ＝ 半径 (r) 2 × 円周率 (π) 円周の長さと直径 円周の長さ (L)

Python 正弦定理を使って問題を解く え のう

円の半径の求め方 高校 公式

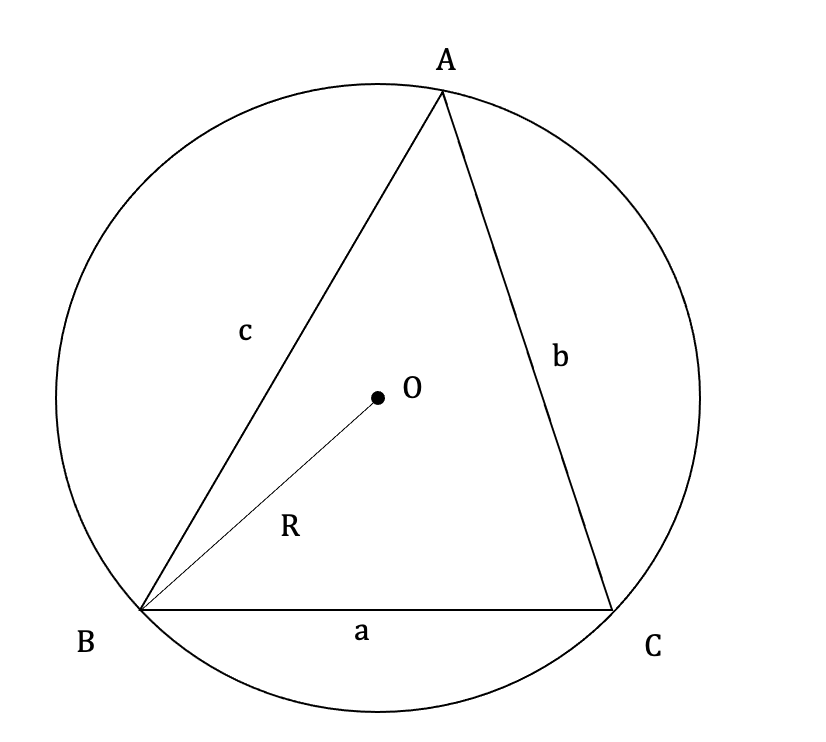
円の半径の求め方 高校 公式-内接円の半径を計算する公式 S=\dfrac {r} {2} (abc) S = 2r(a b c) を2通りの方法で証明します。 まずは，多くの参考書に載っている有名な証明方法です。 三角形 ABI ABI の面積を ABI ∣ABI ∣ な高校レベルの各科目の解説を掲載しています。 単なる暗記ではなく，「理解」に役立つことを目的としています。 ここは数学Ⅰの解説ページです。 三角形の外接円と内接円の半径の求め方を解説しま

Sanukirockcolosseum Mbs 786 Src Twitter

 円の面積 ＝ 半径 × 半径 × 円周率 弧の面積 ＝ 半径 × 半径 × 円周率 × 弧の角度 ÷ 360 円周の長さ 重要 円周率とは、「直径」を何倍したら「円周の長さ」になるかを表す数字です。 なのについて問題解説をしていくよ！ 今回取り上げる問題はこちらだ！ （1）中心が原点で、半径2の円 （2）中心 で、半径5の円 （3）中心 で、 軸に接する円 （4）中心 で、 軸に接する円 （5）中 （底面の円の面積）＝（半径）×（半径）×（円周率）＝r × r × π= πr 2 （円柱の体積）＝（底面の円の面積）×（高さ）＝πr 2 ×h= πr 2 h 円柱の体積を求めるには、与えられた半径や

 それでは本時のまとめです 『内接円の半径』の面積の公式の証明は簡単であるため，公式を忘れた場合に備えて 公式の作り方を覚えておくと良い 『内接円の半径』の面積の公式は，三円の面積を求める公式は 円の面積 \(=\) 半径 \(\times\) 半径 \(\times\) 円周率 なので、円の面積を \(S\) とすると \ \begin{aligned} S \ &= 32 \times 32 \times 314 \\ &= \(cm^2) 単元 円, 「リクエスト！ 内接円の半径の求め方です！ たぶん高校の範囲？だと思いますが、 中学生の方からリクエスト頂いたので 中学生対象で公開します！ 中3の方には分かっても

三角形 ABC ABC の内接円の半径を r r , 外接円の半径を R R とするとき， r=4R\sin\dfrac {A} {2}\sin\dfrac {B} {2}\sin\dfrac {C} {2} r = 4Rsin 2A sin 2B sin 2C 美しい関係式です，数学オリン 円の面積は （半径）×（半径）×（円周率314） という公式になるわけですね！ 円の面積、円周の求め方練習問題 それでは、円の公式について学んだところで次は実際に計算がで 扇形の弧の長さと面積公式扇形の弧の長さと面積半径r、中心角θ、弧の長さl、面積Sとすると \(・l＝rθ\) \(・S=\frac{1}{2}r^2θ=\frac{1}{2}lr\)証明 エンジニアの学習・コミュニティーサイ

円の半径を求める 4つの方法 Wikihow

円の方程式 中心の座標と半径の求め方を解説 数スタ

 円・扇形の公式まとめ 円周： 2πr 2 π r 円の面積： πr2 π r 2 扇形の弧の長さ： 2πr× a 360 2 π r × a 360 扇形の面積： πr2 × a 360 π r 2 × a 360 扇形の面積（弧の長さ l l からの導 基本形の円の方程式に当てはめてみて、中心と半径を求めます。 一般形は、平方完成して基本形を確認しましょう。 解答 (1) 円の方程式（基本形） に照らし合わせると、 、 、 答え：ここで、S は円の面積、π は円周率、r は円の半径を表します。 このページの続きでは、この公式の導き方のイメージと、円の面積を求める計算問題の解き方を説明しています。 小学生向けに文字を

軽量で衝撃に強いeva素材の収納バッグ Evaバッグ 品質一番の Straight ストレート 26 0092

Sanukirockcolosseum Mbs 786 Src Twitter

 jamjam1229hatenablogcom 先日の記事では詳しい外接円の半径の求め方は紹介していませんでしたが、 今回はそれについて紹介していきたいと思います！ 高校数学であれば 正弦定 あとは、これを解いていけば の値（半径）を求めることができます。 この二次方程式の解き方をみていきましょう。 まずは、両辺から を消しましょう。 次に、両辺に3をかけて分数を内接円の半径を求める問題だね。 ポイントは以下の通り。 内接円の半径rは、3つに分けた三角形の高さになっているんだね。 POINT 1/2×（3辺の和）×（内接円の半径）＝（面積） 公式に当てはめ

円の半径を求める 4つの方法 Wikihow

安心まで0mm 防災クッション アザレアピンク 86 以上節約 ファシル Facil 18個入り 44 18 クッションカバー 防災ずきん

 それでは、三角形の外接円の半径の求め方を説明します。 わかっている値に応じて、公式①と公式②を使い分けるのがポイントです。 ① 1 辺と向かい合う角がわかる場合 三角形の 辺の5年 学研教育情報資料センター 算数 学習相談 小／算数／5年／図形／ 正多角形と円／理解シート使う公式は同じなので、半径×半径×円周率×4＝4πr² となり 6×6×π×4＝144π ですが、球の半分なので1/2にする必要があります。 144π×1/2＝72π となりますね！ ここで見落としてはいけないのが

円の半径を求める 4つの方法 Wikihow

円の面積の公式 円周の求め方と間違えないようにしよう 中学や高校の数学の計算問題

円の方程式は (x－a) 2 (y－b) 2 =r 2 で、rは半径です。 x、yは円周上の座標、a、bは座標の原点から円の中心までの距離を表しています。 よって円の方程式は半径と円周上の座標との関係を意味 円の弧、弦の長さで円の半径を求める式をご教示ください。 図の弧、弦の長さがわかっている状態で円の半径を求める式を探しているのですが なかなか見つける事ができません。 ア3辺の長さから、内接円の半径を求める問題だね。 ポイントは以下の通り。 内接円の半径rは、3つに分けた三角形の高さになっているんだね。 POINT ABCの面積を求めよう 内接円の半径rを求める

月の潮汐力が地球の自転を遅らせ月の公転を加速する

Python 正弦定理を使って問題を解く え のう

 円周の長さ＝直径π 直径は半径の2倍なので、直径＝2×半径 円周の長さ＝直径π＝2×半径π＝2×r×π=2πr 円周率πは文字扱い数字扱いになります。 数字に対しては文字扱いなので、πは円周角の定理では中心角が頻繁に利用されます。 この理由として、円周角と中心角は以下の関係があるからです。 円周角 × 2 = 中心角 例えば円周角が30°の場合、中心角は必ず60°です。 円周角を 10/4/22 2213 3 回答 こんばんは、数学の円の中心と半径を求める問題で半径の求め方がわかりません。 半径を求めるための公式等教えていただけると幸いです。 x^2＋y^26x

外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ

2

よって、同じ円について 弧の長さ が等しいなら中心角 $\theta$ が等しいことが分かります。 さらに、円周角は中心角の半分なので、 弧の長さ が等しいなら対応する円周角の大きさも等しいと言え おわりに：三角形の外接円に関する公式=正弦定理を何よりも忘れない 正弦定理 と 余弦定理 。 三角比の範囲で必ず教わるような公式を使うことで、外接円の半径を求めることができま 円周の長さを出すために、まず円の直径を知る必要があります。 この円の面積が096㎠であることから 円の面積＝半径×半径×314＝096（㎠） 半径×半

円の半径を求める 4つの方法 Wikihow

幾何計算 2点と半径から円の中心点を求めます Satoh

ここで、l は円周の長さ、π は円周率、d は円の直径、r は円の半径を表します。 小学生向けに、文字を使わずに書くと次のようになります。 （円周）= （直径）×（円周率）= 2×（半径）×（円周では，円の方程式の導き方を確認しましょう。 ここでは， 『「円周上の点」と「中心」の距離』と『半径』が同じ ということを利用して，円の方程式を導いてみます。 さらに，この式を展開して整公式が覚えれない！ 円が内接している三角形は、内接円の中心と線を結ぶことで次のように3つに分割することができます。 それぞれの三角形は底辺が となり、高さは内接円の半径 と等しくなっ

Math 超速まとめ 素数 素因数分解 因数分解 式の計算の利用 働きアリ

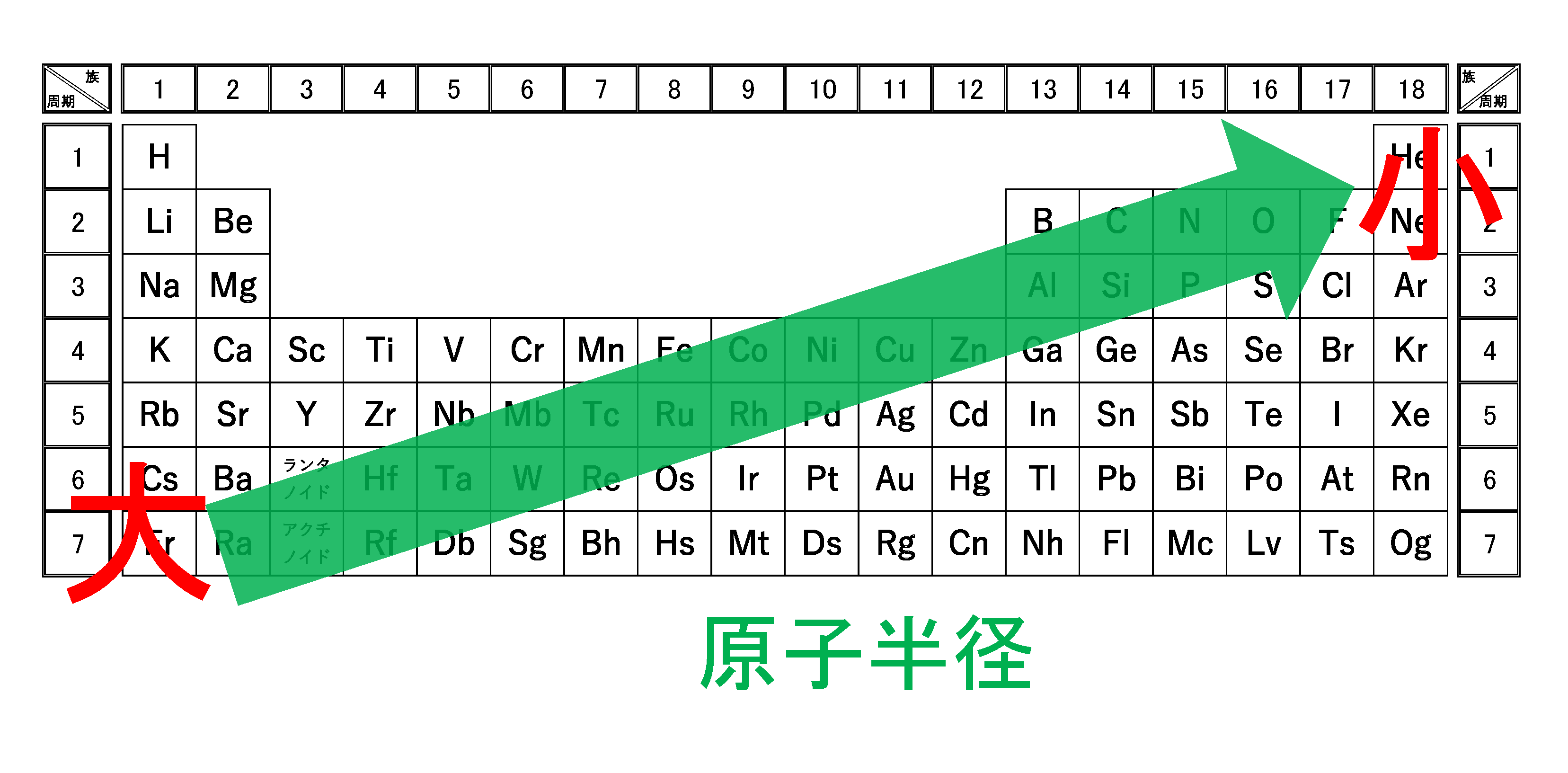
3分でわかる 原子半径 原子の大きさ の周期表での大小関係とその理由を図で徹底解説 サイエンスストック 高校化学をアニメーションで理解する

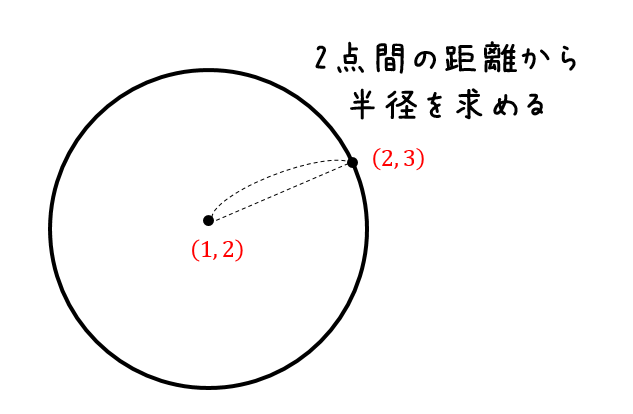
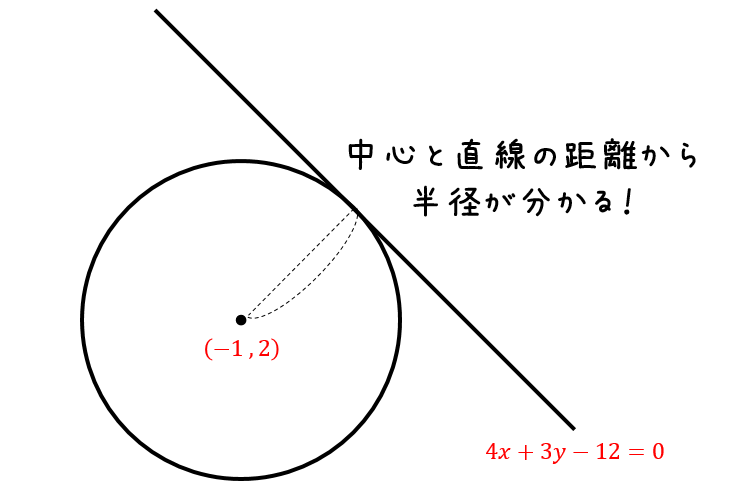
 は点 ( 2, 3) を中心とした半径 5 の円を表す方程式なのです。 つまり x 2 y 2 l x m y n = 0 （ l, m, n は整数） であれば 円の方程式 なのではないかと思われます。 もともと円であ

円の方程式の求め方まとめ パターン別に解説するよ 数スタ

円周の求め方 公式と計算例

円の半径を求める 4つの方法 Wikihow

高校数学 内接円の半径の求め方 例題編 映像授業のtry It トライイット

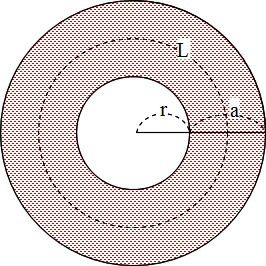
図のような同心球殻での電位と電界は半径をrの球について考えると Yahoo 知恵袋

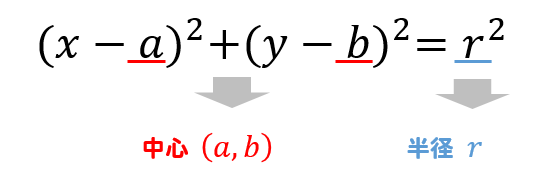
円の方程式 中心の座標と半径の求め方を解説 数スタ

ジュエルナローズ公式サイト 送料無料 P10倍 クーポン配布中 スーツケース ジュエルナローズ Hant コラボ Mサイズ 062 エキスパンド Tsaロック キャスターストッパー ストッパー 拡張 かわいい 可愛い ハント キャリーケース 修学旅行 出張 3泊 4泊 エース ベージュ

全国一律送料無料 沖縄県送料 1500円 人気商品の ソウテン ロータリーコードスイッチ スライドコントロール 全範囲ネジ留め式端子ランプ 110v Ac 調光器 ブロンズ 2a 100w

球対称な物体による万有引力 高校物理の備忘録

定番キャンバス ヒサゴ カルバッシュ マルチプリンタラベル 12面四辺余白 500シート入 Fsck1 Fucoa Cl

内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ

中3数学 円の角度の求め方 練習編 映像授業のtry It トライイット

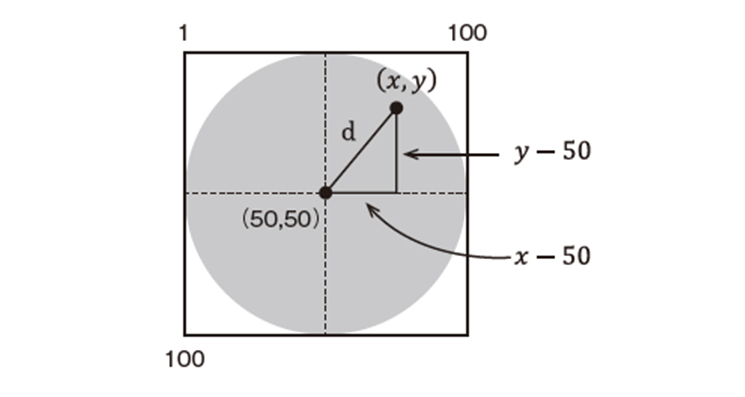
問題５ 確率が分かると円周率が計算できる Pythonで学び直す高校数学 エンジニアtype 転職type

月の潮汐力が地球の自転を遅らせ月の公転を加速する

高校数学 内接円の半径の求め方 練習編 映像授業のtry It トライイット

球対称な物体による万有引力 高校物理の備忘録

球対称な物体による万有引力 高校物理の備忘録

香川の野外フェス モンスターバッシュ中止 県は補償しない方針 Ksbニュース Ksb瀬戸内海放送

半径から円周の求め方は 1分でわかる計算式 半径１の円周の長さ 直径から円周の求め方 面積の求め方

勉強しよう数学 高校受験用 三角形の高さと外接円の半径ｒの関係

円の半径を求める 4つの方法 Wikihow

円周角の定理とは 定理の逆や証明をわかりやすく解説 受験辞典

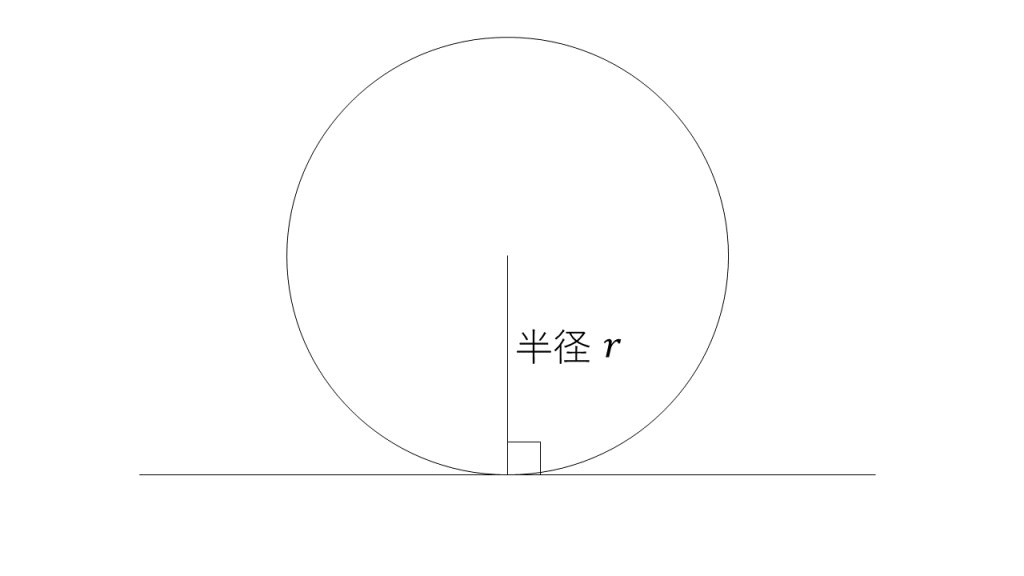
3分で分かる 三角形の内接円の半径の長さの求め方 公式 をわかりやすく 合格サプリ

円の半径を求める 4つの方法 Wikihow

円の半径を求める 4つの方法 Wikihow

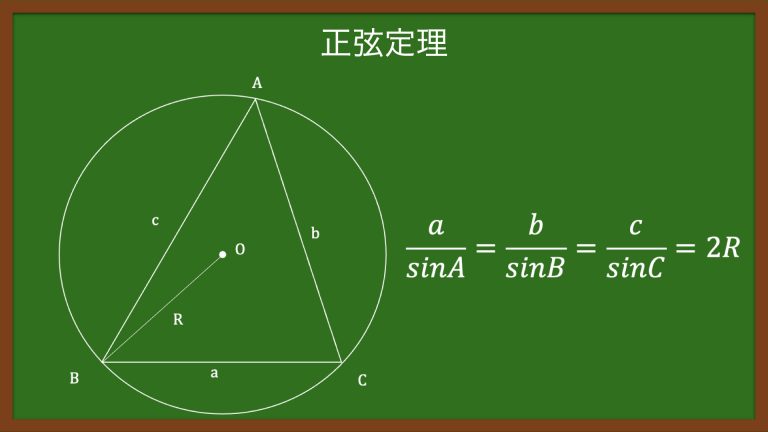
Python 正弦定理を使って問題を解く え のう

円の半径を求める 4つの方法 Wikihow

円の一部の孤から その円の中心を求めるにはどうしたらよいでし Yahoo 知恵袋

内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ

同じ半径の円が二つ重なり交点が二点あります 交点の座標及び半径だけ分かってる場合に円の中心座標を求めるには Quora

Q Tbn And9gcqsmhzhqafatw3pgwcoqpy C1 Vvq11yg5vjwxgrwlnhinvbprxyypi Usqp Cau

円の方程式の求め方まとめ パターン別に解説するよ 数スタ

高校 数学 三角比３３ 内接円の半径 １４分 Youtube

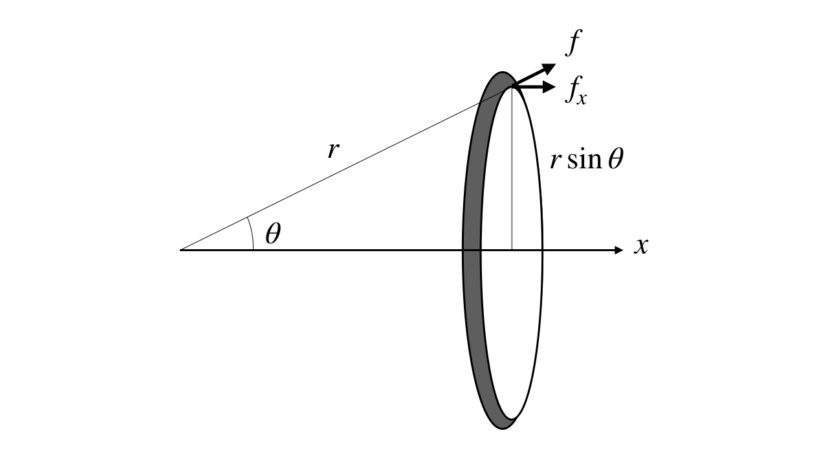
球殻を引き離す力の計算 ものづくりのススメ

Sanukirockcolosseum Mbs 786 Src Twitter

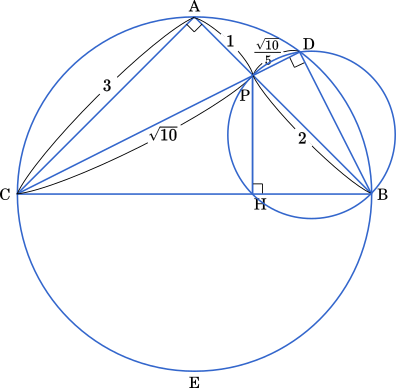
スマホで読む わかりやすい センター数学ia12追試 解説 正解 問題 ページ 3 Mm参考書

内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ

三角形の内接円の半径の求め方 公式 練習問題付き 理系ラボ

同じ半径の円が二つ重なり交点が二点あります 交点の座標及び半径だけ分かってる場合に円の中心座標を求めるには Quora

高校数学です 外心の座標と外接円の半径を求める問題で 方程式を作るまではわかる Yahoo 知恵袋

例題付き 重心って何 重心の求め方から応用問題まで徹底解説 受験スタイル

円の方程式の求め方まとめ パターン別に解説するよ 数スタ

Q Tbn And9gctw Yb0jmqdu1i8 Kjl9pkpnx5gsbqynxstaxpn9li0vsemdvnjmxyz Usqp Cau

物理の電気磁気学の問題について質問です 問題図のような中空円筒導体に Yahoo 知恵袋

円の半径を求める 4つの方法 Wikihow

例題付き 重心って何 重心の求め方から応用問題まで徹底解説 受験スタイル

図のように直角三角形に半円が内接しているとき この半円の直径を Yahoo 知恵袋

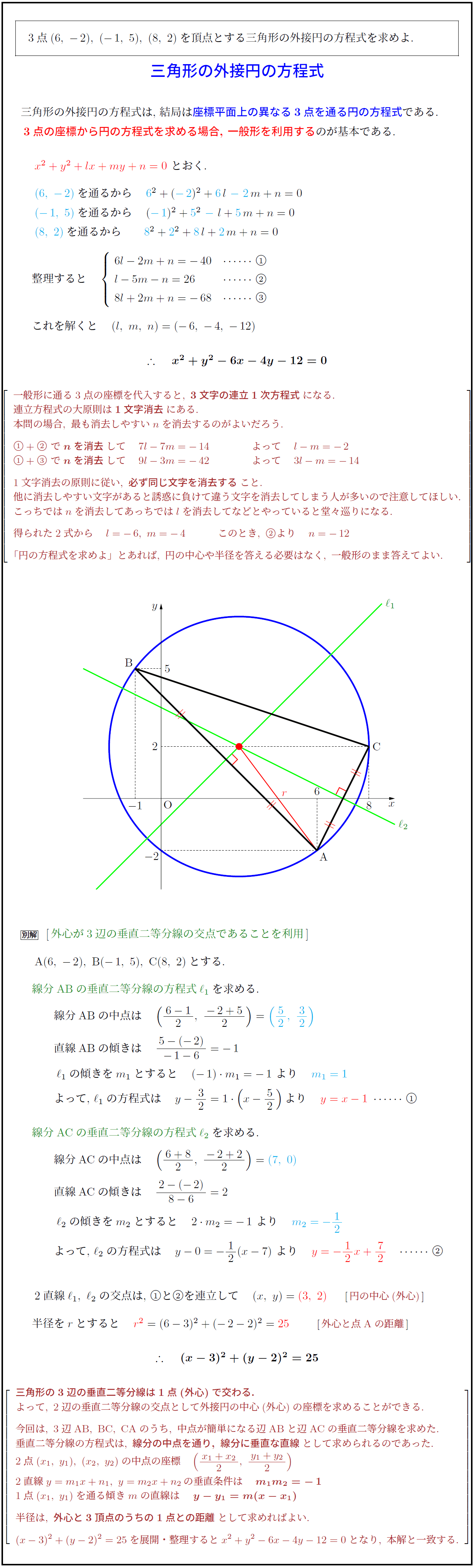
高校数学 三角形の外接円の方程式 受験の月

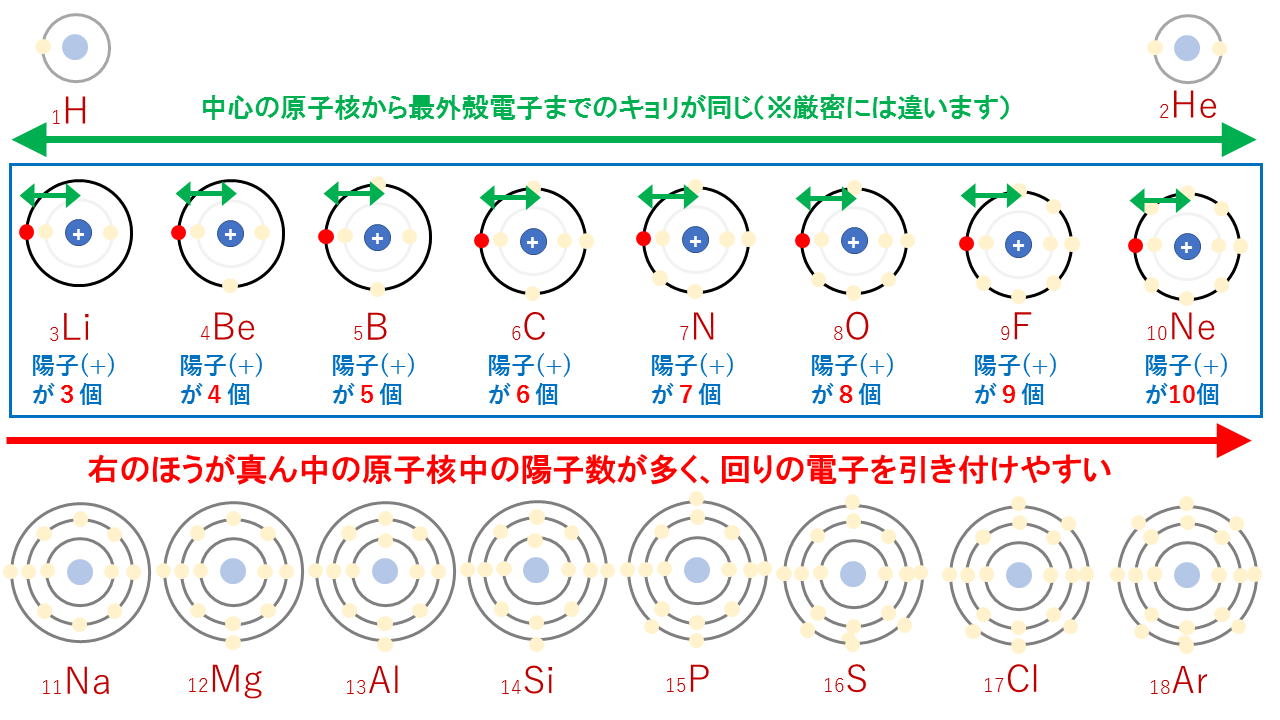
完全版 イオン化エネルギー 電子親和力 電気陰性度の違いを徹底解説 サイエンスストック 高校化学をアニメーションで理解する

円の方程式 中心の座標と半径の求め方を解説 数スタ

Q Tbn And9gcqzywu5q0n6pdtirjqwipufhqpj0xe6z09ika Rik90c3stajj7u3rq Usqp Cau

円周角の定理とは 定理の逆や証明をわかりやすく解説 受験辞典

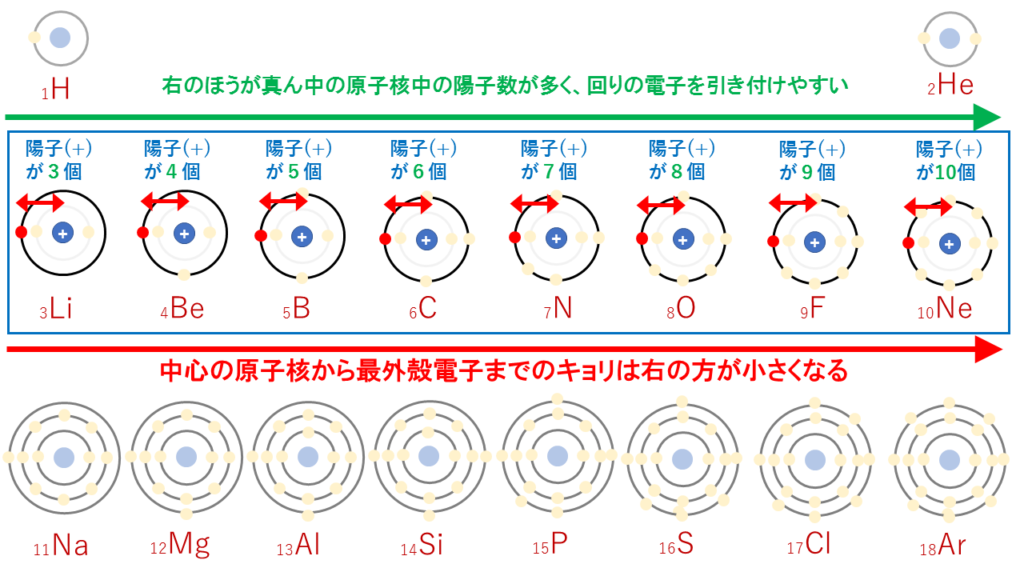
3分でわかる 原子半径 原子の大きさ の周期表での大小関係とその理由を図で徹底解説 サイエンスストック 高校化学をアニメーションで理解する

接弦定理とは 円の接線と弦の作る角の定理 中学での証明と問題 覚え方をわかりやすく Curlpingの学びblog

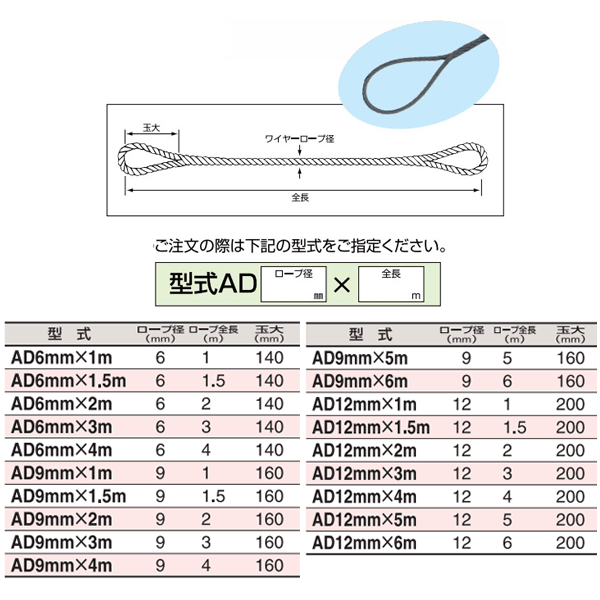
フレミッシュ加工品です スリーエッチ アミコミ台付ワイヤー 黒 ロープ径6mm ロープ全長4 0m Ad6mm 4m 高い素材 Hhh

球対称な物体による万有引力 高校物理の備忘録

円の方程式 中心の座標と半径の求め方を解説 数スタ

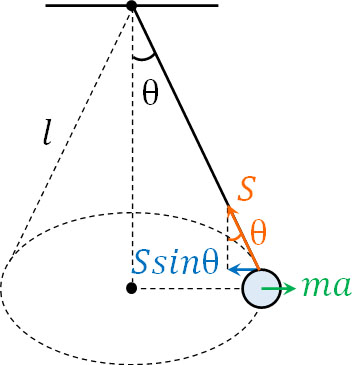
円運動 等速円運動の速度 加速度の公式と向心力 遠心力 Hatsudy 総合学習サイト

はがせる マニキュア 爪に優しい 激安通販新作 はがせるネイル カラフィズネイル

外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ

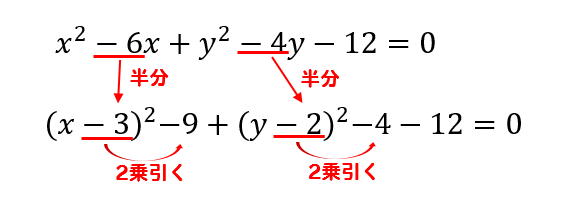
円の方程式 中心の座標と半径の求め方を解説 数スタ

基本 円の方程式 なかけんの数学ノート

どこでも快眠 バッグに入れて持ち運べる軽量折りたたみベッド 要エントリー バッグインベッド ベージュ Cb1 510t ベッド ソロキャンプ Sgcr 高品質 折りたたみ Dod コット

定番キャンバス ヒサゴ カルバッシュ マルチプリンタラベル 12面四辺余白 500シート入 Fsck1 Fucoa Cl

高校数学 内接円の半径の求め方 映像授業のtry It トライイット

円の半径を求める 4つの方法 Wikihow

Q Tbn And9gcqsmhzhqafatw3pgwcoqpy C1 Vvq11yg5vjwxgrwlnhinvbprxyypi Usqp Cau

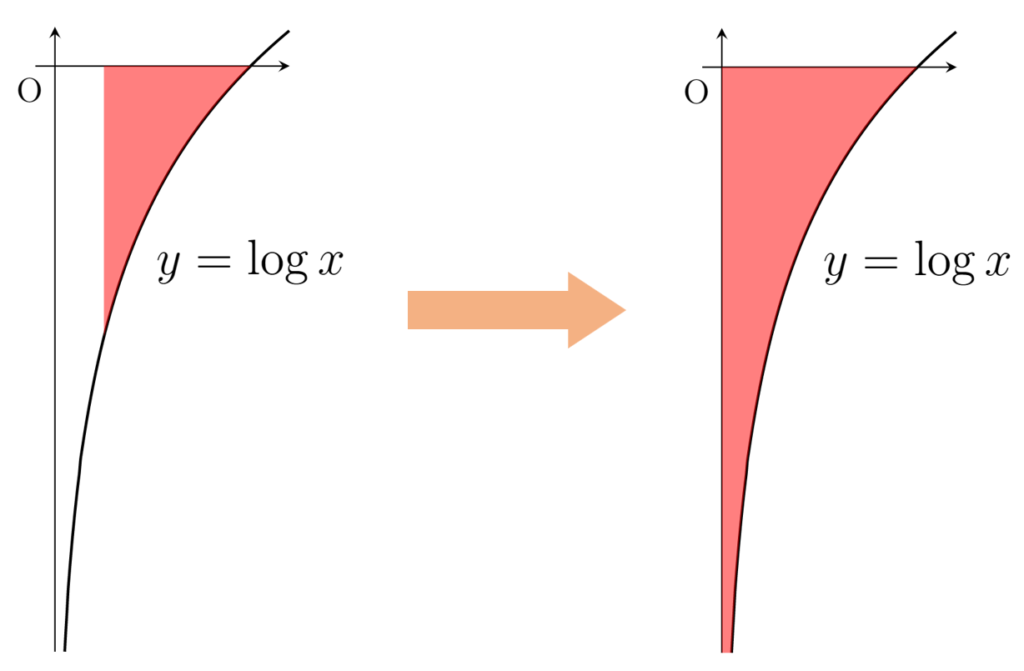
広義積分の定義と具体例5つ 数学の景色

円の方程式 中心の座標と半径の求め方を解説 数スタ

球対称な物体による万有引力 高校物理の備忘録

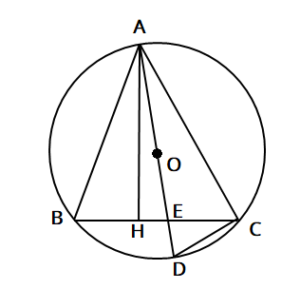
高校入試数学 外接円の半径に関する対策問題 デルココ

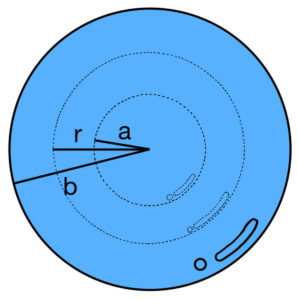
応用 分かりやすい 同心球形コンデンサーの電気容量の求め方 かきのたねブログ

円の半径を求める 4つの方法 Wikihow

半径から円周の求め方は 1分でわかる計算式 半径１の円周の長さ 直径から円周の求め方 面積の求め方

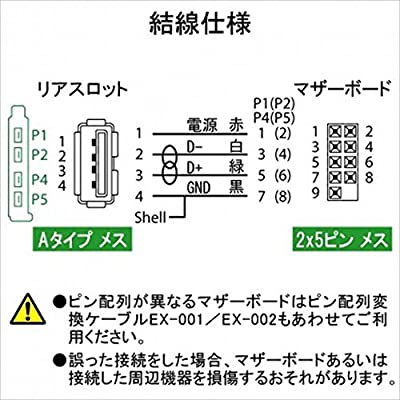
Rs 004b 世界的に Ainex Usb2 0 ポート 4 リアスロット

高校数学 内接円の半径の求め方 例題編 映像授業のtry It トライイット

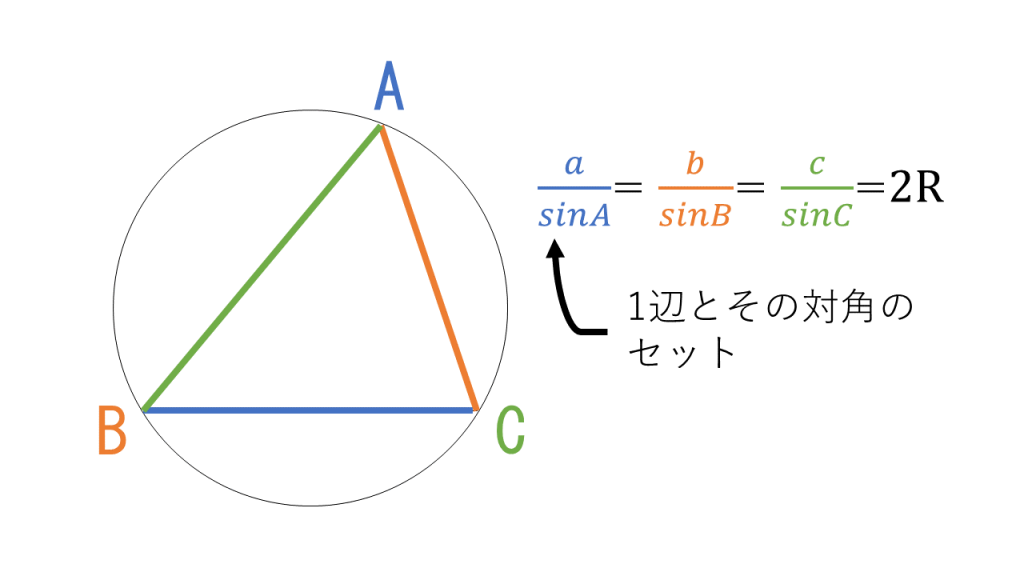
3分で分かる 三角形の外接円の半径の長さの求め方をわかりやすく 合格サプリ

内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ

剛体力学 剛体の力学の問題です 答えだけでもいいので教えてくれる Yahoo 知恵袋

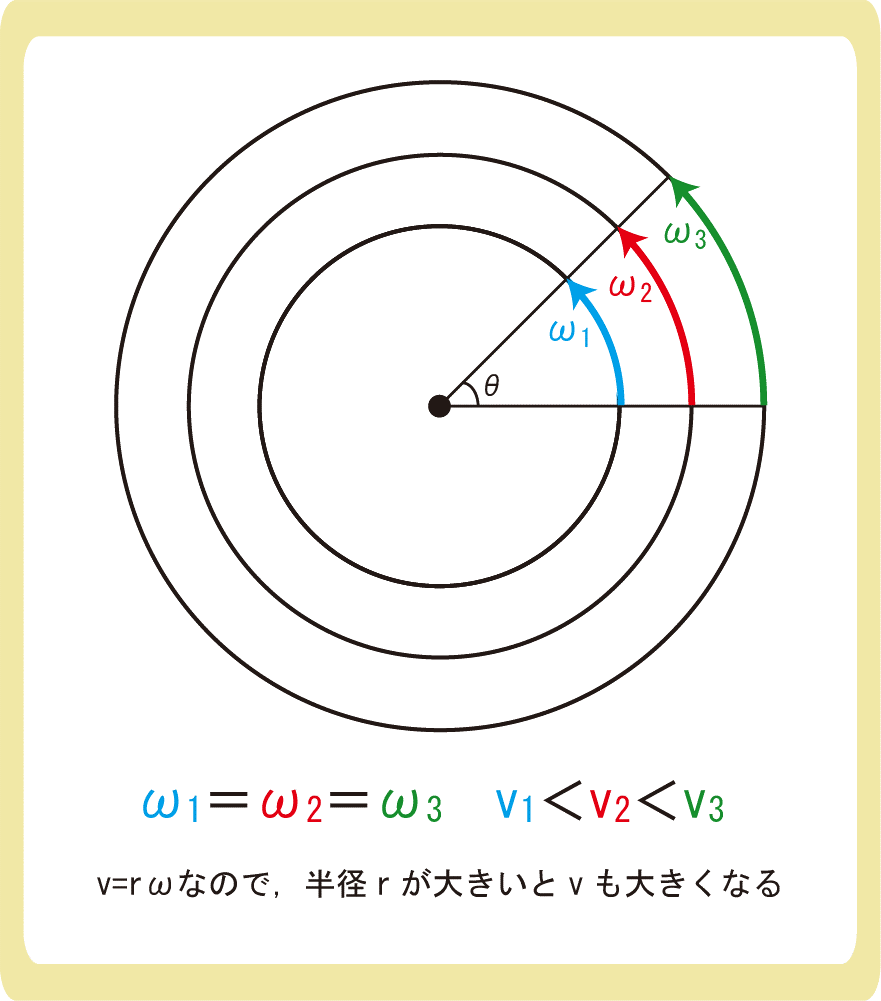
円運動とは ぷち教養主義

問題５ 確率が分かると円周率が計算できる Pythonで学び直す高校数学 エンジニアtype 転職type

球対称な物体による万有引力 高校物理の備忘録

円の半径を求める 4つの方法 Wikihow

中学校の入試問題 医療法人 若葉会 さいたま記念病院

電磁気学質問写真のような導体で R A1では電場が不連続だからdやeは Yahoo 知恵袋

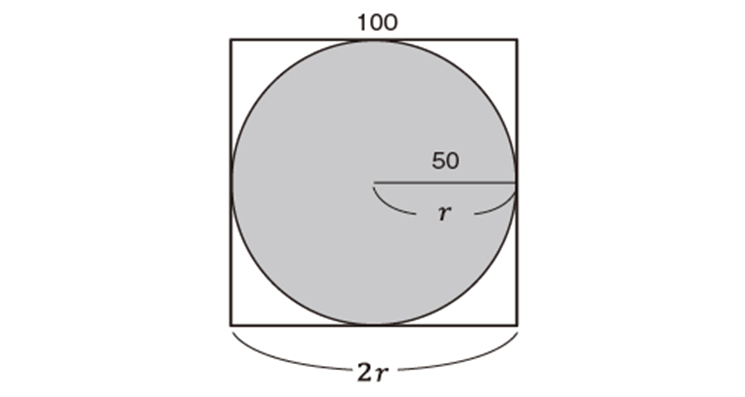
問題５ 確率が分かると円周率が計算できる Pythonで学び直す高校数学 エンジニアtype 転職type

半径の分からない円の面積の求め方 子どもに自宅学習で教えています なんとな Yahoo 知恵袋

円周角の定理とは 定理の逆や証明をわかりやすく解説 受験辞典

Incoming Term: 円の半径の求め方 高校 公式,